The projection, together with information about the position and extent of the raster map, gives you a rule how to convert a latitude and longitude into a map pixel position. Furthermore, you will have to make sure that the co-ordinates you are getting from your GPS and the raster map use the same map datum. If you do not know what a map datum is, again, follow the link above. GPSes normally use the WGS-84 map datum. My GPS can be set to use any other datum as well, but the downloaded output will always be WGS-84. Not having the right map datum can introduce errors of hundreds of metres.
In my case, I could safely assume that the map I got was using the "British Grid", a transverse Mercator projection with certain parameters, based on a 1936 Ordnance Survey map datum; this is commonly used in Britain. I had to find algorithms to convert the WGS-84 output of my GPS to grid values which was not too difficult.


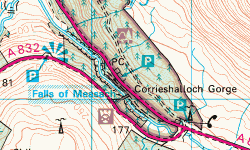
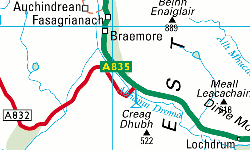
These pictures show Braemore Junction as depicted on the 1:50 000 Ordnance Survey maps, and on the digital Bartholomew road map (probably something like 1:250 000 in comparison) which I am using on my site.
Do not look at the absolute size - look at the relative properties. Look at the shape of the A832 as it leaves the junction to the left, or look at how wide the gap (the Corrieshalloch Gorge) between the roads is, measured in road-widths. It is probably about six road-widths on the OS map, and only two on the Bartholomew map!
What this example tells you is that map makers cheat. They have to cheat if they want to create readable maps; they have to paint roads wider or narrower or further apart. They have to smoothe some bends, change some angles. Sometimes of course they are plain wrong, as in this comparison where the Bartholomew folks have put the village of Achnasheen on the wrong side of the roundabout:
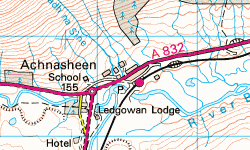
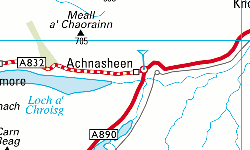
And see how the railway station is further north than the roundabout on the OS map, and further south than the roundabout on the Bartholomew version? And see how far away from the road the river is?
Since your GPS does not know about all these dirty little map maker's secrets, you will end up with points that do not fit your map exactly (unless your map is very accurate indeed - and in that case the GPS errors will trouble you).
This approach works for reasonably small stretches of GPS track, say, up to 20 by 20 kilometres. Anything larger, and you are likely to encounter problems - whenever you've got one end of the track right, the other won't match and vice versa.
I still have problems where two roads are so close together that GPS errors may cause a measurement taken on one road to be closer to the "wrong" road than to that where it should be; there's some manual fiddling involved in solving these. As a "last resort", I can also manually correct the computed pixel position for a photo's co-ordinates but I try to use that as little as possible.