4. Electronic Cash

Aus den in diesem Vortrag vorgestellten Konzepten einer "Signatur" und einer "Hashfunktion" lassen sich bereits funktionierende eCash-Systeme entwickeln.

Zuvor seien jedoch die wünschenswerten Eigenschaften elektronischen Geldes zusammengefaßt:

Unabhängigkeit:
Das Geld darf nicht an einen physischen Ort gebunden sein und muß immateriell - z.B. im Internet - übertragbar sein.
Sicherheit:
Das Geld darf nicht fälsch- bzw. kopierbar sein.
Schutz der Privatsphäre:
Wie beim Bargeld soll niemand feststellen können, wer welche Geldeinheit wann wo ausgegeben hat.
Offline-Fähigkeit:
Wird das Geld ausgegeben, ist in diesem Augenblick keine Verbindung zu einem Zentralrechner (z.B. der Bank) notwendig.
Übertragbarkeit:
Das Geld soll frei auch zwischen Personen übertragbar sein, d.h. der Weg "Bank-Käufer- Verkäufer-Bank" darf nicht vorgeschrieben sein.
Teilbarkeit:
Das Geld soll beliebig in kleinere Einheiten aufgeteilt werden können.

Dies sind wünschenswerte Eigenschaften. In diesem Vortrag werden wir kein eCash-Verfahren vorstellen können, das allen diesen Forderungen genügt.

4.1 Das einfachste digitale Geld

Zum Einstieg in das Thema stellen wir zunächst ein ganz einfaches Verfahren für digitales Geld vor. Wir verwenden dabei die Begriffe "Zettel" und "aufschreiben", weil das Beispiel so anschaulicher wird; tatsächlich "digital" wird das Geld natürlich nur, wenn man eine elektronische Form der Nachrichtenspeicherung und -Übermittlung benutzt. Alle Protokolle funktionieren selbstverständlich auch papierlos.

Alice fordert von der Bank einen Geldschein an.
Die Bank schreibt auf einen Zettel "Dies sind DM 100,-" und signiert den Zettel, indem sie ihn (oder eine Hashfunktion davon) mit ihrem privaten Schlüssel verschlüsselt. Gleichzeitig bucht sie DM 100,- von Alices Konto ab.
Alice besitzt jetzt einen "Geldschein" und trägt ihn zu Bob in den Laden (sie kauft Band 1 von D.E. Knuths "The Art of Computer Programming" im Sonderangebot).
Bob prüft den "Schein", indem er ihn mit dem öffentlichen Schlüssel der Bank entschlüsselt. Es klappt, also weiß Bob, daß der Schein tatsächlich von der Bank verschlüsselt bzw. signiert wurde und daher "echt" ist.
Bob reicht den Zettel bei der Bank ein; diese erstattet ihm die DM 100,- auf sein Konto.

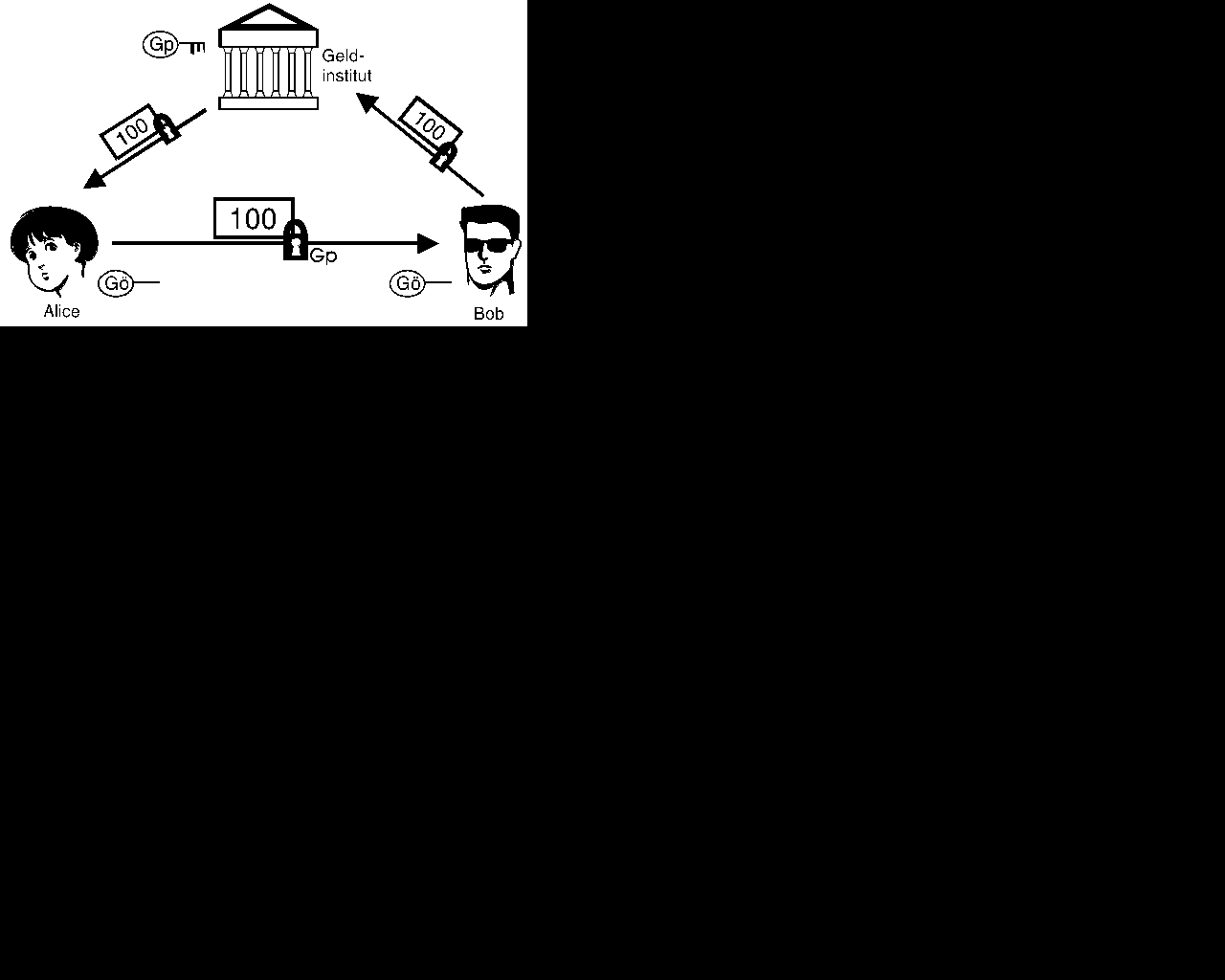
Bei diesem simplen Verfahren tritt zunächst das Problem auf, daß Alice und Bob beliebig viele Kopien des Scheins anfertigen und ausgeben können. Die Bank muß also eine eindeutige "Seriennummer" einführen, die sie auf alle Scheine druckt.

Dadurch entstehen jedoch zwei neue Probleme:

Die Bank kann, wenn Bob den Geldschein einreicht, feststellen, daß er von Alice kam. Ist Alice Ordensschwester und Bob Inhaber eines zwielichtigen Video-Shops, sammelt sich bei der Bank schnell brisante Information an. Diese Information wird zwar heute bei bargeldlosem Zahlungsverkehr auch gespeichert, ist jedoch gesellschaftlich problematisch und sollte, wenn sie nicht zur technischen Abwicklung nötig ist, gar nicht erst erzeugt werden.
Das Geld ist nicht "Offline-fähig", denn Bob weiß nicht, ob Alice denselben Schein evtl. schon woanders ausgegeben hat und die Bank seine Einlösung daher platzen läßt. Bob muß sofort bei der Einlösung des Scheins bei der Bank rückfragen, ob diese Seriennummer tatsächlich noch nicht eingelöst wurde.

4.2 Digitales Geld mit "Blinding Factor"

Der "Blinding Factor", den wir nun einführen wollen, ist eine erstaunliche Idee, die aber bei genauerem Hinsehen durchaus gut funktioniert. Wieder ziehen wir für unser Beispiel (genauer gesagt, ein Beispiel von David Chaum, dem Erfinder des "Blinding") Umschläge und Zettel heran, zu den mathematischen Grundlagen kommen wir später.

Alice schreibt auf 100 Zettel: "Dies sind DM 100,- ", und versieht jeden mit einer Seriennummer, die so lang, ist, daß die Wahrscheinlichkeit, daß jemand anders dieselbe benutzt, sehr gering ist.
Sie verpackt alle 100 Zettel in Umschläge und legt jeweils noch ein Kohlepapier ein.
Alices Bank öffnet 99 von den 100 Umschlägen und vergewissert sich, daß Alice nicht gelogen hat. War Alice in 99 Fällen ehrlich, nimmt die Bank an, daß auch im 100. Umschlag das Richtige steht, unterschreibt blind den 100. Umschlag und bucht DM 100,- von Alices Konto ab.
Alice kann den Geldschein wie vorher ausgeben.
Die Bank löst später den Schein ein, ohne zu wissen, daß er von Alice kommt. Wenn der Schein mit der gleichen Seriennummer bereits eingelöst wurde, weist die Bank ihn zurück.

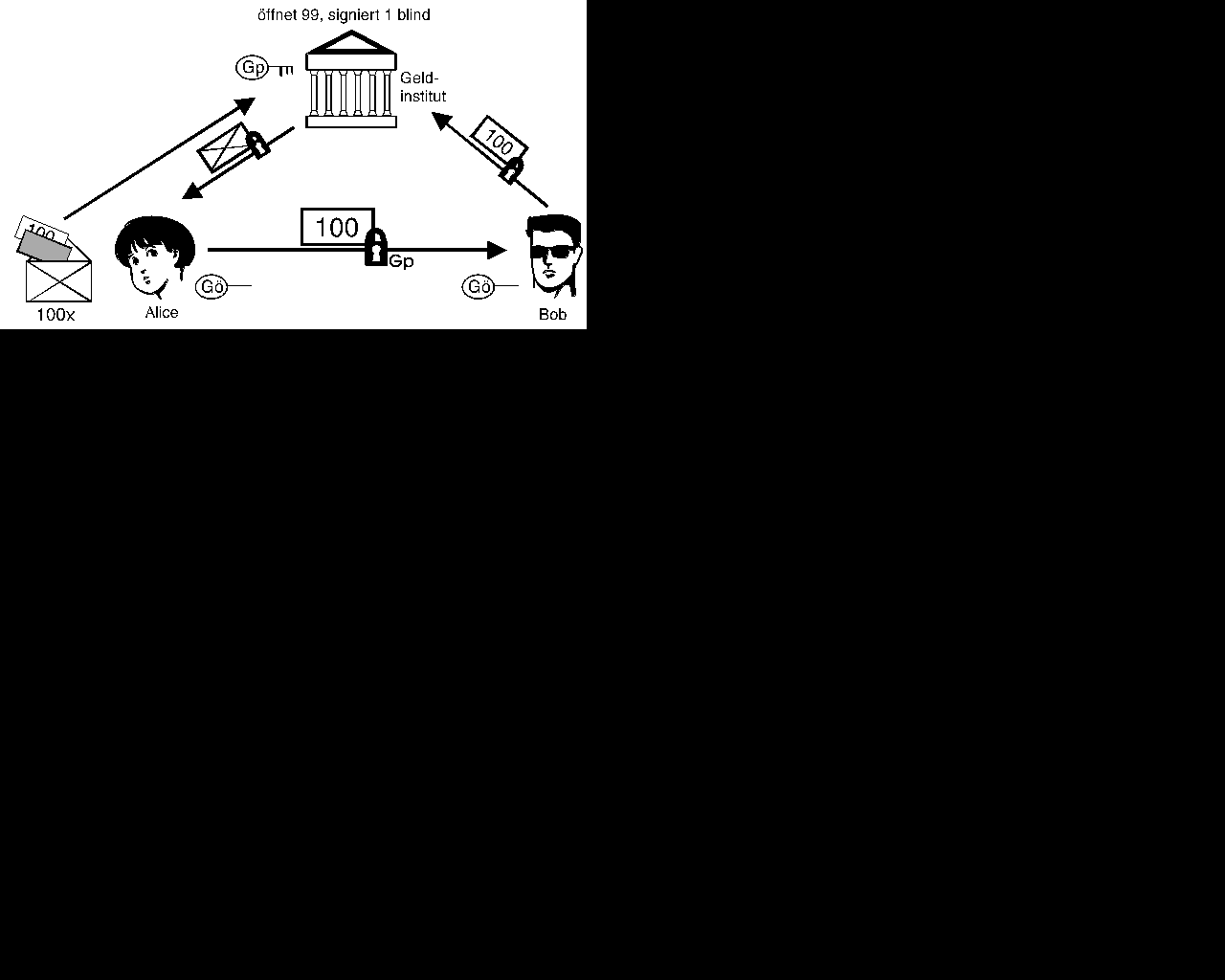
Diese Protokoll löst das Problem der Verfolgbarkeit; Alice kann nun ihr Geld ausgeben, ohne daß jemand später weiß, wo das geschah. "Offline-fähig" ist das neue Geld aber immer noch nicht, denn es ist nicht sichergestellt, daß Alice den gleichen Geldschein nicht mehrmals ausgibt. Auch Bob könnte das tun, und dann wäre nicht einmal klar, ob Alice oder Bob nun falsch spielen. Daher muß wie zuvor beim Bezahlen bereits die Bank gefragt werden, ob dieser Schein noch gültig ist.

4.3 Mathematische Erklärung des Blinding Factor

Legt man zur Verschlüsselung den asymmetrischen RSA-Algorithmus zugrunde, läßt sich das "Blinding" wie folgt mathematisch erklären:

Die Bank besitzt

den öffentlichen Schlüssel e,
einen privaten Schlüssel d,
einen öffentlichen Modulus n.

Liebe HTML-Leser: Wenn das hier kaum leserlich scheint, weil die Exponenten nicht dargestellt werden, laden Sie bitte das entsprechende GIF-Bild!)

Verschlüsselt die Bank eine Nachricht m, so bildet sie üblicherweise m^d mod n und muß dazu natürlich die ursprüngliche Nachricht m im Klartext besitzen. Will Alice nun aber eine Nachricht von der Bank verschlüsseln lassen, ohne daß die Bank sie lesen kann, geht man so vor:

Alice wählt eine beliebige Zahl k zwischen 1 und n. Dann verdeckt sie ihre Nachricht m durch
t = mk^e mod n
Die Bank verschlüsselt die verdeckte Nachricht t:
t^d = (mk^e)^d mod n
Alice deckt t^d auf durch
s = t^d/k mod n
...und sie erhält
s = m^d mod n

(Zum Verständnis ist wichtig, daß gilt: (x^e)^d = x.) Alice besitzt also am Ende genau die Nachricht s, die sie auch erhalten hätte, wenn die Bank die ursprüngliche Nachricht m auf "normale Weise" mit Kenntnis des Klartexts verschlüsselt hätte; die Bank allerdings kann, da sie den "Blinding Factor" k nicht kennt, nicht sehen, was sie verschlüsselt.

4.4 Digitales Geld mit Schutz vor Mehrfach-Ausgabe

Zur Absicherung gegen das mehrfache Ausgeben desselben Geldscheins müssen wir zunächst ein neues Konzept einführen: Das sogenannte "Secret Splitting". Beim "Secret Splitting" wird eine Nachricht in beliebig viele einzelne Teile zerlegt und ist nur dann wieder lesbar, wenn man alle Teile besitzt. Dabei ist durch Kryptographie sichergestellt, daß man nicht, wie etwa bei einem zerissenen Blatt Papier, aus Teilen der Nachricht auf das Ganze schließen kann.

Wir sind nun an einem Punkt, an dem die "Papier-Analogie" nicht mehr hundertprozentig greift, weil inzwischen solche Datenmengen erzeugt werden müssen, daß niemand sie mehr auf einen Zettel schreiben kann; dennoch halten wir noch einmal daran fest.

Alice erzeugt für dieses Protokoll zunächst eine Information I, die ihre Identität verrät, z.B. "Ich bin Alice Ryder und wohne in der Bahnstraße 28 in 12345 Berlin". Mit einem Secret-Splitting-Protokoll erzeugt sie hieraus 10.000 mal ein Tupel (I1, I2)x. Kennt man zwei zusammengehörige I, kann man die Original-Information lesen; sonst nicht.

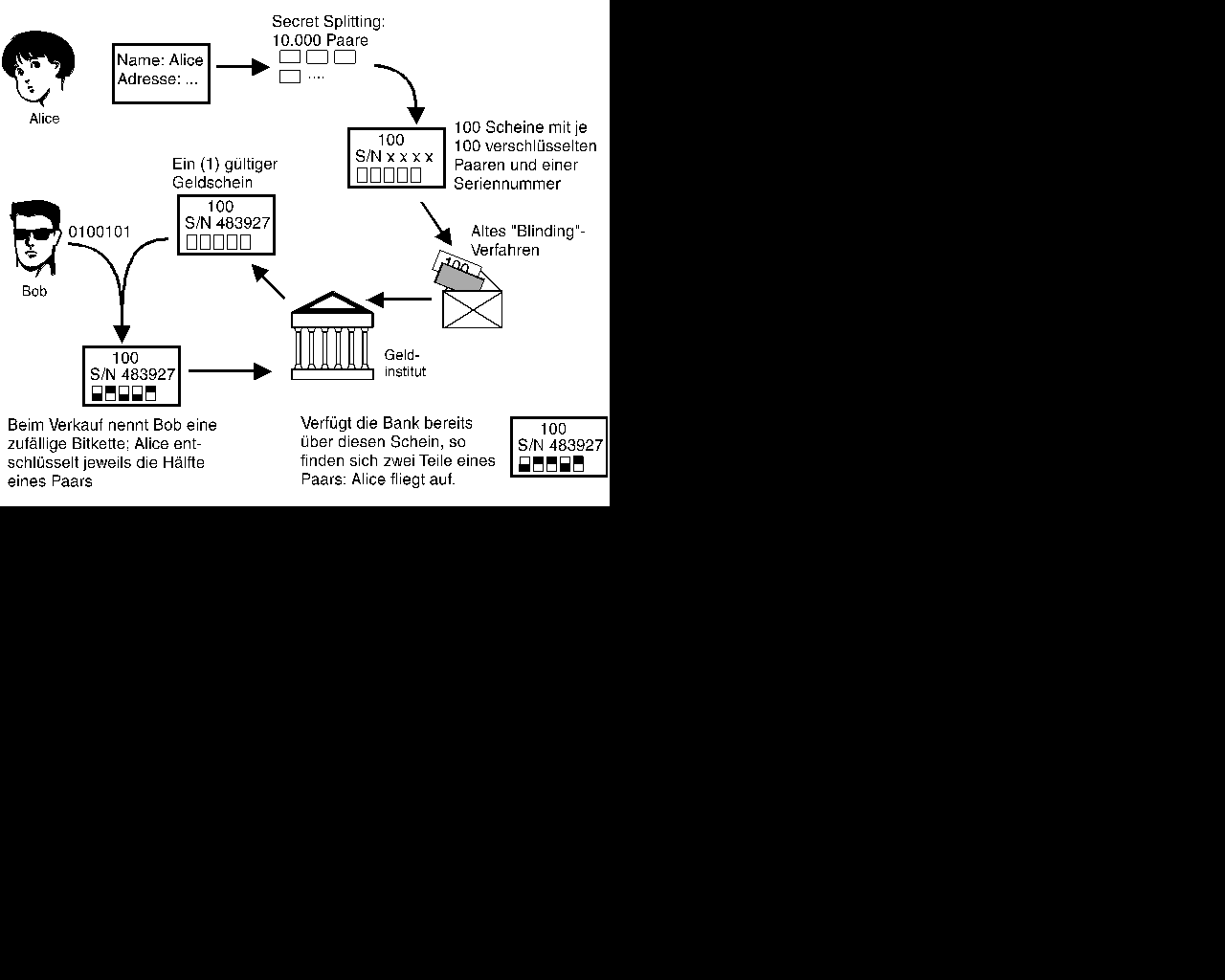
Alice erzeugt wie gehabt 100 Zettel mit 100 Seriennummern. Zusätzlich schreibt sie auf jeden Zettel die beiden Hälften von 100 I-Paaren in verschlüsselter Form.
Sie verpackt, ebenfalls wie vorher, alle 100 Zettel in Umschläge und legt jeweils noch ein Kohlepapier ein.
Alices Bank öffnet 99 von den 100 Umschlägen und vergewissert sich, daß Alice nicht gelogen hat; dazu muß Alice die I-Paare auf allen 99 Zetteln entschlüsseln, damit die Bank sieht, daß (bei allen 9900 Paaren!) tatsächlich die richtige Identität herauskommt. Ist das der Fall, unterschreibt sie blind den 100. Umschlag und bucht DM 100,- von Alices Konto ab.
Alice kann den Geldschein, der nun 100 verschlüsselte I-Paare enthält, wie vorher ausgeben. Der Händler Bob bittet sie dabei, aus jedem der 100 I-Paare je eine Hälfte zu entschlüsseln (welche Hälfte, legt der Händler anhand eines Zufallsgenerators fest). Bob kann zwar nachvollziehen, ob die Entschlüsselung richtig vorgenommen wird (ob Alices Schlüssel "paßt"), kann mit den dadurch entstehenden unverschlüsselten Hälften jedoch nichts anfangen, da er wegen des "Secret Splitting" auch die zweite Hälfte, die ja noch verschlüsselt ist, benötigt.
Die Bank löst später den Schein ein, ohne zu wissen, daß er von Alice kommt.
Wenn Alice versucht, den Schein mehrfach auszugeben, fällt dies in dem Moment auf, in dem Bob den Schein einlöst. Die Bank merkt das an der gleichen Seriennummer und holt den bereits eingelösten Schein aus der Datenbank. Dann vergleicht sie die I-Paare beider Scheine. Die Wahrscheinlichkeit, daß genau die gleichen Hälften auf beiden Scheinen "geöffnet" (entschlüsselt) sind, ist sehr gering. Viel wahrscheinlicher ist, daß der Händler, bei dem Alice den Schein vorher bereits ausgegeben hat, sie bei mindestens einem I-Paar eine andere Hälfte öffnen ließ. Dadurch hat die Bank nun aber von diesem I-Paar bide Hälften, kann sie zusammensetzen und erhält Alices Identität - eine halbe Stunde später steht bereits die Polizei vor ihrer Tür. Wie man sieht, verhindert dieses Verfahren nicht, daß ein Geldschein mehrfach ausgegeben wird - aber es stellt sicher, daß die Übeltäterin zur Verantwortung gezogen werden kann, wenn sie es probiert.

Zurück
Weiter